Reinforcement Learning

Key

states $s_{i}$
actions $a_{i}$
rewards $R$
discount factor $γ \in [0, 1]$ : specifies the relevance in the present of future rewards.
return $G$ : cumulative reward
policy $π$ : a specification of how the agent acts. $π (a | s)$ gives the probability of taking action $a$ when in state $s$ .

The goal of reinforcement learning is to choose a policy $π (s) = a$ that will tell us which action to take in state $s$ so as to maximize the expected return.

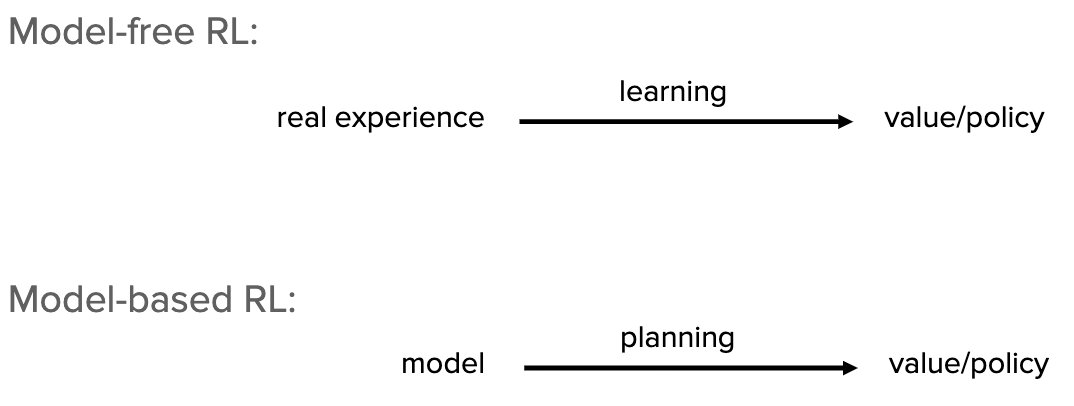
RL Overview

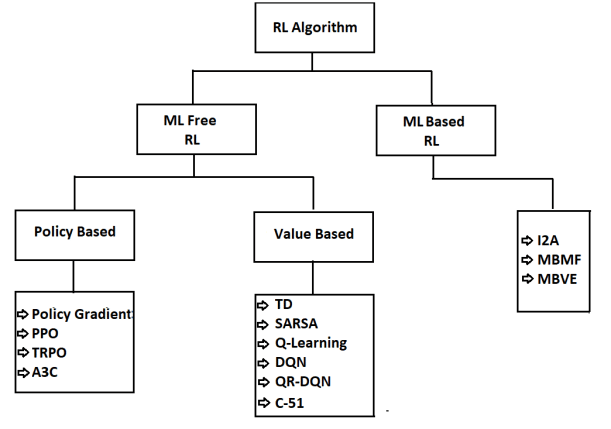
Model-based vs. Model-free RL

Value-based vs. Policy-based RL

differs in the types of algorithms used to derive the optimal behavior

Value-based RL: estimates the expected cumulative reward (i.e. value) of being a certain state and choosing to take a certain action
Policy-based RL: learns the policy to optimize a parametrized policy function with gradient ascent to maximize the expected cumulative reward

Off-policy vs. On-policy methods

differs in whether the agent is using the newest policy that is being updated

Off-policy methods
- estimate values that are not based on the agent's current policy. Most often, values are estimated under the assumption of optimal future behavior (i.e. optimal policy).
- Q-learning is an example of off-policy learning algorithm.
On-policy methods
- estimate values under the agent's current policy, including possible randomness/stochasticity in future behavior (e.g. ε-greedy)
- SARSA (State-Action-Reward-State-Action) is an example of on-policy learning algorithm
- note not all policy-based RL are on-policy

Q-Learning

It is a type of reinforcement learning: model-free. value-based, and off-policy

Concepts

Q value: the expected cumulative reward for taking an action in a particular state.
State-action value function (Q function)
- it specifies how good it is for an agent to perform a particular action in a state with a policy $π$
- Q function takes input of the state-action pairs and outputs the Q-values
- math forms: Q(s, a) = Return, if you
  - start in state $s$
  - take action $a$ (once, to $s^{'}$ )
  - then behave optimally after that
Bellman equation = the sum of reward at the current state and the return from behaving optimally starting from the state $s^{'}$ :

How it works

the agent selects the action with the highest Q-value in each state
after each step, the policy is evaluated and the Q-values are updated using the Bellman equation
the process is repeated until the policy converges and selects the same action at a given state

Algorithms

Upper Confidence Bound

UCB is a deterministic algorithm for Reinforcement Learning that focuses on exploration and exploitation based on a confidence boundary that the algorithm assigns to each machine on each round of exploration. These boundary decreases when a machine is used more in comparison to other machines.

example: which Ads customers will click on

How it works

At each round n, we consider two numbers for machine m:
- N(n) = number of times the machine m was selected up to round n.
- R(n) = number of rewards of the machine m up to round n.
From these two numbers we have to calculate,
- The average reward of machine m up to round n, $$r(n) = R(n) / N(n)$$
- The confidence interval $[r (n) — Δ (n), r (n) + Δ (n)]$ at round n with,

Δ (n) = \sqrt{1.5 * l o g (n) / N (n)}

We select the machine m that has the maximum $U C B = r (n) + Δ (n)$

Intuitive explanation
https://medium.com/analytics-vidhya/upper-confidence-bound-for-multi-armed-bandits-problem-ea5d7bc840ff

Thompson Sampling (Bayesian Bandits)

How it works

At each round n, we consider two numbers for machine m:
- $N_{i}^{1} (n)$ = number of times the ad $i$ got reward 1 up to round n.
- $N_{i}^{0} (n)$ = number of times the ad $i$ got reward 0 up to round n.
For each ad $i$ , we take a random draw from the beta distribution below:

3. We select the ad that has the highest $\theta_i (n)$   # Markov decision process The core reinforcement learning approaches define the world as a Markov decision problem, which is built on hidden dynamics and optimal control.  $$G = R_i + \lambda R_{i+1} + \lambda^2 R_{i+2} + \lambda^3 R_{i+3}+ ...

...until termination.